дал автору, совершавшему первые шаги на поприще импульсных источников, ведущий специалист ООО «Мега-электроника» А. И. Колпаков: «Надо самому изучать техническую документацию, читать книги и много думать». Того же пожелаю и вам, уважаемые читатели. Берите в руки карандаш и лист бумаги, готовьте паяльник и — в путь!

Автор выражает благодарность Е. Родикову (г. Новосибирск), Е. Батракову (г. Орск), А. А. Зуеву, В. А. Могучему, И. П. Соснину, П. А. Семенову, А. Г. Ракову. Без участия этих людей книга вряд ли бы появилась на свет.

Магнитные материалы, используемые в импульсной технике, их основные свойства

...Мне тут трансформатор импульсный понадобился, килогерц эдак на 50. Взялся я его посчитать как классический 50-герцовый. Здорово так получилось — и габариты, и витки. Хорошо, что делать не стал! Открываю случайно одну мудрую книжку, а там — это нельзя, то нельзя. Используйте какие-то низкокоэрцитивные материалы, потери в магнитопроводе считайте. Целая наука в общем. Разобраться бы...

1.1. Основные характеристики магнитного поля

Прежде чем рассказать, какие магнитные материалы подходят для применения в импульсной технике, как их правильно выбрать и правильно использовать, давайте вместе вспомним кое-что из курса физики, касающееся электромагнетизма [12]. Нам необходимо иметь четкое представление об основных величинах, характеризующих магнитные взаимодействия, чтобы оценивать магнитные материалы и рассчитывать моточные изделия (дроссели, трансформаторы). Итак, начнем.

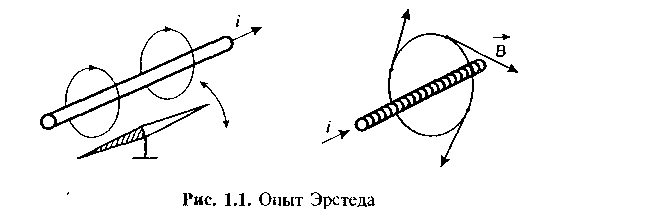
Впервые существование магнитного поля у проводника с током обнаружил Эрстед в 1820 году. Опыт Эрстеда нам знаком со школьной скамьи — проводник располагается вблизи магнитного компаса, и когда по проводнику пропускают ток, стрелка компаса отклоняется от своего первоначального положения. Изменение направления тока заставляет поворачиваться стрелку в противоположную сторону.

Давайте пока забудем о проводнике с током как об источнике магнитного поля — сейчас для нас совершенно неважно, что создает его. Представим себе некое пространство, в котором существуют силовые линии магнитного поля. Чтобы охарактеризовать величину магнитного поля в пространстве, было введено понятие магнитной индукции (В).

Магнитная индукция — векторная величина. Это значит, что ее вектор направлен по касательной к силовой линии магнитного поля.

Существует еще одна характеристика магнитного поля, называемая напряженностью магнитного поля (Н). Об этой характеристике можно и не вспоминать, пока мы рассматриваем силовые линии свободного магнитного поля. Физики говорят о таком поле как о поле «в вакууме». Но как только мы начинаем исследовать поле, силовые линии которого проходят в веществе, мы будем удивлены — картина меняется коренным образом. В этом случае мы будем вынуждены ввести дополнительные характеристики. Объясняется это тем, что любое вещество, будь то металл, жидкость или газ, в той или иной мере является магнетиком, то есть способно под действием внешнего поля намагничиваться, приобретать собственный магнитный момент. Читатель наверняка удивится: «Разве воздух, окружающий нас, тоже может притягивать к себе предметы, подобно тому, как притягиваются железки к магниту?» Да, любое вещество может участвовать в магнитных взаимодействиях, однако в разной степени, и об этом мы поговорим чуть позже. А сейчас вернемся к нашему полю в пространстве. Намагниченное вещество создает магнитное поле В_в, которое накладывается на внешнее поле В₀. Оба поля в сумме дают результирующее поле:

Для объяснения намагничения тел ученые предложили теорию, согласно которой в молекулах вещества циркулируют круговые микроскопические токи. Каждый такой ток создает в окружающем пространстве магнитное поле. При отсутствии внешнего поля молекулярные токи ориентированы беспорядочно, вследствие чего результирующее поле равно нулю. Под действием поля магнитные моменты иолекул, которые можно представить похожими на детские волчки,

ориентируются в одном направлении. Магнетик намагничивается, приобретая магнитный момент, отличный от нуля. Магнитные поля отдельных микроскопических токов уже не компенсируют друг друга и возникает поле В_в.

Намагничение магнетика характеризуют магнитным моментом единицы объема—намагниченностью (J). Теоретически намагниченность представляет собой понятную физическую величину. Казалось бы, бери магнитный момент отдельного молекулярного микротока, относи его к малому' объему', взятому в окрестности рассматриваемого молекулярного тока, суммируй получившиеся величины по объему всего тела — и вот они, исчерпывающие сведения о поле внутри тела...

Однако в практических расчетах мы столкнемся с непреодолимым затруднением. Чтобы определить индукцию В, нам необходимо иметь исчерпывающую информацию fie только о токах, создающих внешнее поле, но и о молекулярных токах, которые, в свою очередь, зависят от результирующей индукции В. Поэтому физики поступили следующим образом — они нашли вспомогательную величину, которую можно определить, пользуясь только информацией о внешних макроскопических токах, намагничивающих вещество. После несложных преобразований можно получить следующее выражение:

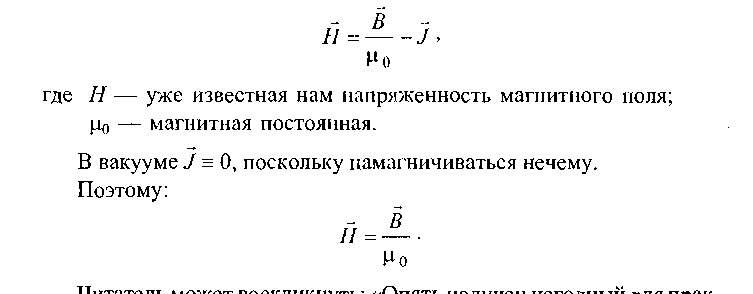
*1ша1сль милс1 виычлшчпу 1ь. чиил1ь пилу пси пс1 идныи длл ирак-

тики результат! Как я смогу вычислить намагниченность? Да и работать с векторами непросто». Не стоит спешить с выводами. Дело в том, что введение вспомогательной величины Н позволяет нам воспользоваться так называемой «теоремой о циркуляции вектора Н», которая постоянно будет помогать нам при расчетах конструктивных параметров дросселей и трансформаторов.

Звучит теорема следующим образом: «Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме микпоскопических токов, охватываемых этим контуром»:

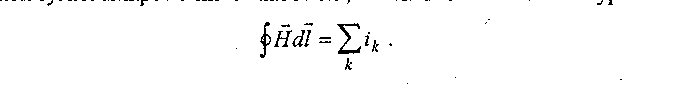
Вычислять интегралы интересно далеко не всем, мало того, нужно уметь их вычислять, чтобы получить правильный результат. Как же быть читателю, который пока не на «ты» с высшей математикой? Давайте осмыслим эту сложную на первый взгляд теорему, и она покажется нам весьма подходящей для практики. Наверняка, вы, уважаемый читатель, держали в руках ферритовое колечко, широко использующееся в импульсной технике. Если колечко достаточно тонкое, тогда длину его средней линии по окружности обозначим I. Через колечко проходят провода с токами г',, /₂... Теперь представим наше кольцо состоящим из маленьких бусинок, нанизанных на линию /. В каждой бусинке мы можем определить величину вектора Я, умножив его по соответствующим правилам на маленький элемент длины бусинки сїї, как показано на рис. 1.2. Оговоримся сразу, что интегрирование —- это не что иное, как суммирование вычисленных величин по всем бусинкам.

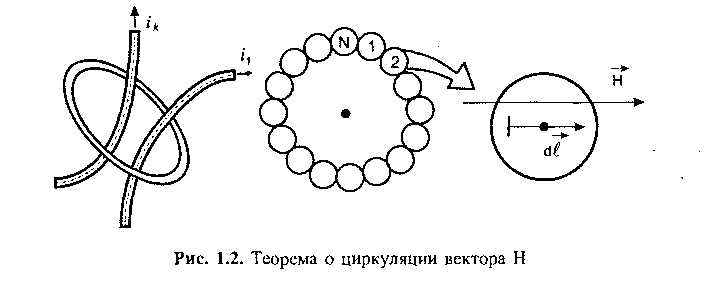
Если мы пробежимся по всему контуру /, то заметим, что от бусинки к бусинке взаимное расположение вектора напряженности и элемента длины не меняется. Поэтому имеем право в данном частном случае не вычислять подынтегральное выражение для каждой бусинки, а просто записать: _

Зная длину контура и силы токов, проходящих через этот контур, мы «на лету» вычисляем напряженность магнитного поля в контуре. Запомним этот результат.

Теперь нам нужно воедино связать намагниченность У, магнитную индукцию В и напряженность магнитного поля Н. Следует отметить, что процессы, происходящие в магнетиках, чрезвычайно сложны. Их анализу посвящены тысячи фундаментальных научных работ, десятки тысяч научных статей. Нам, конечно, нет никакого смысла углубляться во все премудрости электромагнетизма. Практиков всегда вполне устраивают простые допущения, позволяющие с достаточной точностью оценить ту или иную физическую величину, чтобы на основе этих оценок воплощать свои идеи «в железе».

Традиционно намагниченность принято связывать не с магнитной индукцией, а с напряженностью поля. Полагают, что в каждой точке

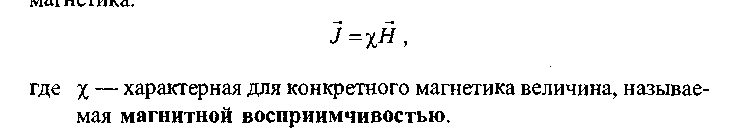
Опыт показывает, что для слабомагнитных веществ при не слишком сильных полях х не зависит от Н. С учетом этого:

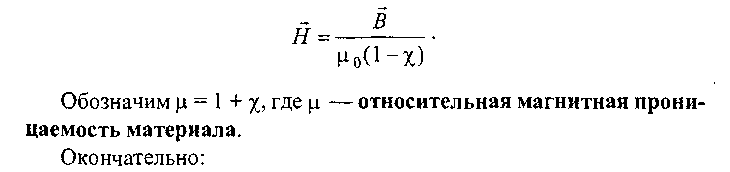
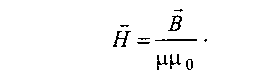
Важный вывод, который мы делаем из этого соотношения, таков: напряженность магнитного поля Н есть вектор, имеющий то же направление, что и вектор В, но в рр₀ раз меньший. Этот вывод справедлив для однородных магнитных сред, когда магнетик равномерно распределен по объему. Для наших расчетов это допущение вполне сгодится. В дальнейшем мы забудем о существовании В, х, а также о том,

что магнитные характеристики являются векторными величинами, и будем использовать в расчетах только В, Н, р.

Пусть имеется однородное поле В₀, созданное в некотором пространстве. Напряженность этого поля:

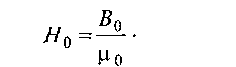
Внесем в это поле, как показано на рис. 1.3, длинный круглый однородный стержень, изготовленный из магнетика, расположив его вдоль направления В₀. Возникающая в стержне намагниченность будет направлена в ту же сторону, что и внешнее поле. В результате поле внутри стержня:

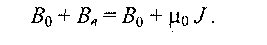
Теперь мы можем определить напряженность поля внутри стержня:

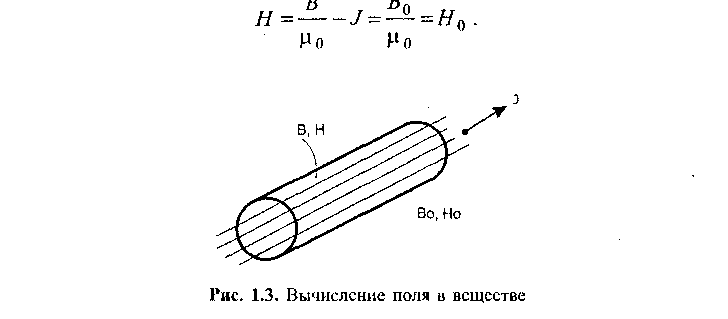
Магнитная индукция внутри стержня:

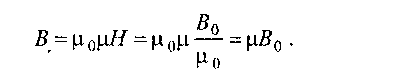
Теперь ясно, что характеризует магнитная проницаемость. Она показывает, во сколько раз усиливается поле в магнетике.

Внимание! Для понимания последующих глав необходимо, чтобы не возникало никакой путаницы в терминологии. Поэтому запомните, что есть:

Замечание для любознательных. До сих пор мы рассматривали достаточно длинные и тонкие стержни. Это допущение вполне подходит для длинных сердечников, а также замкнутых магнитопроводов. Но встречаются случаи, когда стержень имеет соизмеримые геометрические размеры, к примеру, стержневой сердечник дросселя. В этом случае напряженность поля внутри магнетика и вне его не совпадают:

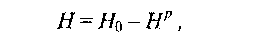
где Н^р — так называемое размагничивающее поле, которое полагается пропорциональным намагниченности:

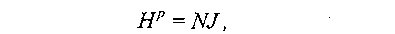
где Ж—размагничивающий фактор, зависящий от формы магнетика.

Для многих тел простой формы (цилиндры, эллипсоиды и т.д.) размагничивающие факторы определены точно. На основе этих выводов строится расчет параметров индуктивных элементов, выполненных на стержневых сердечниках конечной длины. По ходу книги мы столкнемся с такими электротехническими изделиями.

Теперь, разобравшись в основных характеристиках магнитного поля, перейдем к рассмотрению магнитных материалов. Нас мало интересуют свойства таких веществ, как диамагнетики (р < 1) и парамагнетики (р > 1). У одних проницаемость чуть меньше единицы, у других — чуть больше. Разработчик силовой техники едва ли будет про-

ектировать магнитопровод силового трансформатора из латуни, золота или платины. С равным успехом можно было бы вообще отказаться от магнитопровода, то есть намотать обмотки на пластмассовый каркас.

Нас, как практиков, интересует класс материалов, называемый ферромагнетиками. Ферромагнетики являются сильномагнитными веществами — их намагниченность может до Ю¹⁰ раз превосходить намагниченность диа- и парамагнетиков!

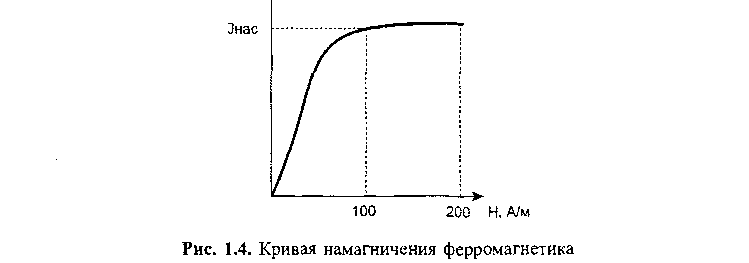
Как мы знаем, намагниченность слабомагнитных веществ изменяется с напряженностью внешнего поля линейно. К сожалению, намагниченность ферромагнетиков зависит от Я сложным образом. Обратим внимание на основную кривую намагничения ферромагнетика, изображенную на рис. 1.4. Магнитный момент этого ферромагнетика первоначально был равен нулю, что очень важно. В данном случае в поле до 100 А/м намагниченность возрастает почти линейно, но после 100 А/м наступает так называемое состояние насыщения, когда с увеличением внешнего поля намагниченность уже перестает расти. Этот эффект говорит о нелинейности магнитных характеристик ферромагнетика.

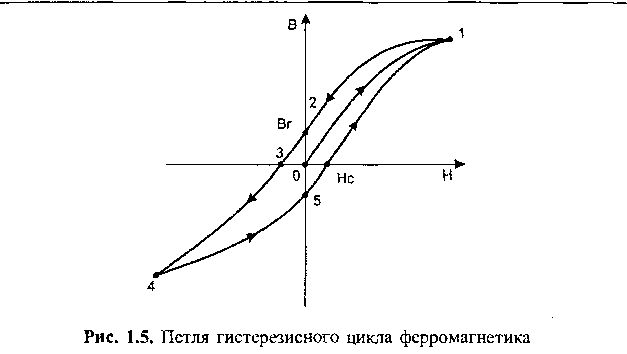
Кроме нелинейной зависимости между Я и /, а следовательно, и между Я и В, для ферромагнетиков характерно наличие гистерезиса. Давайте подробно рассмотрим это фундаментальное свойство ферромагнитного материала, графически изображенное на рис. 1.5, тем более что позже мы будем постоянно сталкиваться с ним.

Итак, предположим, что имеется нейтральный, то есть полностью размагниченный, ферромагнетик. Мы будем постепенно намагничи-

вать его, следя за внутренним состоянием. Результаты поместим на график, по горизонтальной оси которого отложим напряженность внешнего поля, а по вертикальной оси — магнитную индукцию внутри ферромагнетика.

Первоначальное намагничение ферромагнетика до насыщения пройдет по кривой 0-1. После этого мы должны убрать внешнее поле, то есть снизить его напряженность до нуля. Казалось бы, индукция должна вернуться тоже в нулевую точку... Однако ферромагнетик размагничивается по кривой 1 -2, сохраняя при отсутствии внешнего поля магнитный момент, характеризующийся величиной магнитной индукции В_г, называемой остаточной индукцией. Запомним название этого очень важного параметра.

Индукция обращается в нуль лишь под действием внешнего поля Н_с, имеющего направление, противоположное полю, вызвавшему намагничение. Напряженность Н_с называется коэрцитивной силой. Запомним и это название.

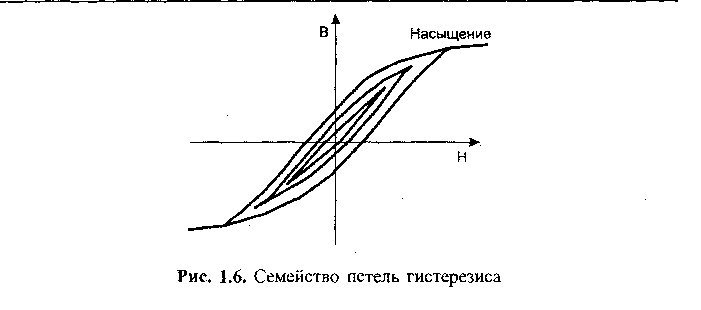
При действии на ферромагнетик переменного магнитного поля индукция меняется по кривой 1-2-3-4-5-1, которая и носит название петли гистерезиса. Если максимальные значения Н таковы, что намагниченность достигает насыщения, ферромагнетик перемагничи-вается по предельной петле гистерезиса. Все петли, находящиеся внутри предельной петли, называются частными циклами. Семейство петель гистерезиса, ограниченных предельным циклом, изображено на рис. 1.6.

Поскольку мы не можем однозначно определить зависимость В от Н, понятие магнитной проницаемости применяется только к основной кривой намагничения. У ферромагнетиков она зависит от напряженности внешнего магнитного поля, как показано на рис. 1.7.

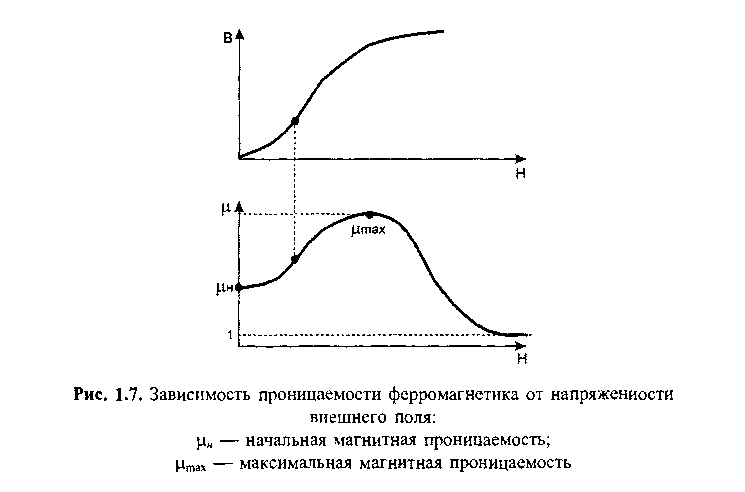
Видно, что максимальное значение проницаемости и достигается при приближении к области насыщения, после чего, при дальнейшем увеличении Н, начинается ее падение. Какой практический вывод можно сделать из этого? Во-первых, проектируя индуктивный эле-

мент, нужно строго следить за индукцией насыщения, чтобы магнито-провод или сердечник не потерял своих полезных магнитных свойств. И, во-вторых, использовать в расчетах значение начальной магнитной проницаемости, а не максимальной.

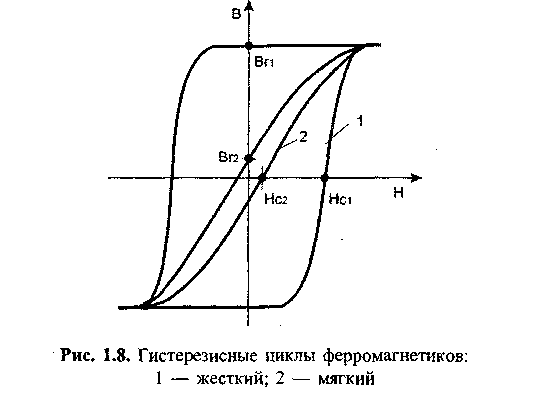
Величины В_г и //. являются основными техническими характеристиками ферромагнетика. Чаще всего разработчику даже не столь интересен вид петли гистерезиса конкретного материала, сколько значение остаточной индукции и коэрцитивной силы. Если //.. велика, ферромагнетик называется жестким (кривая 1 на рис. 1.8). Такой материал подойдет для проектирования постоянных магнитов, однако для магнитопроводов и сердечников индуктивных элементов он не годится совершенно. Для этих целей можно использовать только материалы с мягкой петлей гистерезиса (кривая 2 на рис. 1.8). Почему? Об этом мы поговорим в главе, посвященной остаточной индукции и методам ее снижения.

Еще один немаловажный параметр, который следует учитывать при инженерном проектировании, — это потери на гистерезис. В переменном магнитном поле часть его энергии всегда уходит на пере-магничивание, в результате чего сердечник или магнитопровод нагревается. Потери на гистерезис однозначно связаны с площадью петли гистерезиса — чем больше площадь, тем больше потери.

Используются технологии uCoz

Материал взят из книги

Скачать оригинал КНИГИ в хорошем качестве