Материал взят из книги

Скачать оригинал КНИГИ в хорошем качестве
Теперь настало время узнать, каким образом в компьютерных системах представляются цифры. Во всех современных вычислительных системах это делается, как описано ниже. Представим себе некий узел вычислительной системы. Допустим, он должен передавать на последующие узлы числа в электронном виде. Для этого такой узел имеет группу выходов (обычно их количество равно или кратно восьми). Обозначим эти выходы, как это принято в вычислительных системах, О0...О7 (рис. 2). Эти выходы подключаются к соответствующим входам последующего узла, как показано на рис. 3. Для передачи числа используется вся группа выходов одновременно.
Передаваемое число представляется в двоичной системе счисления. Каждый из выходов передает один разряд двоичного числа и может находиться в одном из двух состояний: состояние логического нуля — когда напряжение на выходе отсутствует, и состояние логической единицы — когда на выходе присутствует напряжение (обычно равное напряжению питания). Причем схема сделана таким образом, что исключает появление на любом из выходов промежуточных значений напряжения. Такая группа выходов называется цифровой шиной данных.
каждый разряд шины имеет свои «вес», сэоычно ии ооозначают разряд, который имеет самый маленький «вес» — вес, равный единице. Это значит, что когда в этом разряде установлена логическая единица, а во всех остальных разрядах логический ноль, то все число равно единице. Разряд 01 имеет «вес» равный двум (102). Это означает, что, если значение разряда 01 равно единице, а всех остальных разрядов — нулю, то все число, передаваемое шиной, будет равно двум. Вес 02 — четыре единицы (1002). И так далее. Вес последнего разряда шины (07) равен 128 (100000002). Для того, чтобы узнать, какое число установлено на шине данных, нужно сложить веса всех разрядов, значение которых в данный момент равно единице.
Очевидно, что для передачи максимально возможного числа нужно установить все разряды шины данных в единичное состояние. В этом случае число, передаваемое по нашей шине данных, будет равно 255 (1 + 2 + 4 + 8+ 16 + 32 + 64 + 128 = 255). Таким образом, по восьмиразрядной шине данных можно передавать числа от 0 до 255 (то есть 256 разных значений). Запомним это, так как восьмиразрядная шина является своего рода стандартом в вычислительной технике. Более подробно к описанию шин мы вернемся, когда перейдем к описанию микропроцессорной системы. А сейчас остановимся подробнее на двухуровневом сигнале, имитирующем двоичный разряд числа.
Каждый из этих уровней имеет свое название. В зависимости от его значения различают сигнал логического нуля и сигнал логической единицы. Другое название — высокий логический уровень и низкий логический уровень. Эти термины в дальнейшем будут часто встречаться в нашей книге.
Для получения сигналов логической единицы и логического нуля используются так называемые триггерные схемы, или схемы с двумя устойчивыми состояниями. Напряжения на выходе любого реального устройства не идеальны и имеют разброс в значениях. Например, сигнал для микросхем, выполненных по так называемой ТТЛ технологии (транзисторно-транзисторная логика), допускают следующие отклонения (при напряжении питания 5 В):
■ Для логического нуля на выходе допускается присутствие напряжения до 0,4 В.
■ Для логической единицы напряжение на выходе должно быть не менее 2,4 В.
По ТТЛ технологии выполнены микросхемы таких серий, как 155, 555, 533, и др. В других типах микросхем уровни сигнала имеют другие значения. Однако существует правило, верное для любых типов цифровых микросхем: если напряжение на выходе цифровой микросхемы входит в заданный диапазон для данного типа микросхем, то другая микросхема, та, на которую приходит цифровой сигнал, надежно распознает ноль или единица у нее на входе. Это происходит благодаря тому, что у цифровых входов имеется так называемый порог срабатывания.
Если входной сигнал выше порога, внутренний триггер устанавливается в состояние логической единицы. Если входное напряжение ниже порога, то триггер переходит в состояние логического нуля. Триггер — это как раз такое устройство, которое может находиться лишь в одном из двух состояний. Среднего не дано. Такой подход повышает надежность работы цифровых схем. Благодаря триггерному эффекту такие явления, как тепловые шумы, дрейф нуля и электромагнитные помехи гораздо меньше влияют на качество передачи цифрового сигнала. Вернее, они вообще не влияют, пока уровень сигнала помехи не превысит порога. Правда, если помехи все же превысят порог, то наступает полный сбой. В этом случае цифровой сигнал, передаваемый по шине данных, будет полностью потерян.
Однако при цифровой передаче сигнала полностью отсутствуют такие эффекты, как постепенное ухудшение качества с увеличением дальности передачи информации и количества перезаписей с одного носителя на другой.
Для обработки цифровых сигналов существует множество схем, которые позволяют хранить цифровую информацию и осуществлять ее преобразование. Например, пользуясь описанными выше правилами, над электронными цифрами можно производить любые арифметические операции, такие как сложение, вычитание, умножение, деление.
Можно делать такие специфические операции, как инвертирование, поразрядный сдвиг и т.д. Данная книга ставит своей’целью подробно рассмотреть, как это делается. А основой для построения подобных схем являются так называемые логические элементы. В следующей главе мы с ними и познакомимся.
Что же это за волшебные элементы. Если вы хоть немного сталкивались с цифровыми схемами, вы наверняка знакомы с логическими элементами. Вы знаете, что на схеме логический элемент обозначается небольшим прямоугольником, имеющим несколько входов и один выход. В настоящее время цифровые микросхемы получили такое большое распространение, что логические элементы можно встретить в схемах очень далеких от микропроцессоров и вычислительной техники. Кроме того, вы наверно встречались и с другими, более сложными элементами цифровой техники: триггерами, дешифраторами, мультиплексорами, счетчиками, регистрами, и т.д. Кто-то знает и понимает, как это все работает и для чего предназначено. А кто-то еще нет. Я считаю необходимым остановиться на этом подробнее. Те, кто знаком с данной темой, могут пропустить несколько разделов.
Для остальных я расскажу все с самых азов. Из всего разнообразия цифровых элементов большинство можно отнести к разряду составных. Составные эти элементы в том смысле, что их можно составить из других, более простых. А в основе всего разнообразия цифровых элементов лежат всего три простейших логических элемента. На рис. 4 изобоажены эти той кита пийюовой техники.
Для изображения логических элементов я придерживаюсь стандарта схемных обозначений, принятых в свое время в СССР, и теперь еще широко используемых во всех странах СНГ. По этим стандартам цифровые элементы изображаются в виде прямоугольника. Все входы рисуются слева, а выходы — справа. Именно таким образом в этом стандарте можно отличить входы элемента от его выходов. Правда, в случае более сложных элементов это правило соблюсти не всегда возможно, так как часто бывает, что один и тот же выход служит одновременно и входом. Но для простых элементов это условие всегда соблюдается.
В западных схемах Приняты другие условные обозначения. В задачи настоящей книги не входит изучение западных стандартов.
Все элементы работают с цифровыми сигналами. Это значит, что сигнал на любом из входов элемента должен принимать значения либо логического нуля, либо логической единицы. На выходе каждый элемент также обеспечивает цифровой сигнал, который, в зависимости от логики работы схемы, принимает значение либо логической единицы, либо дорического нуля. На рис. 4 изображены двухвходовые варианты элемента «И» и элемента «ИЛИ». На самом деле эти элементы могут иметь любое количество входов. Теоретически количество входов может быть увеличено до бесконечности. Дело не в количестве входов, а в логике работы элемента.
Рассмотрим этот вопрос подробнее.
Элемент «И». На выходе этого элемента сигнал логической единицы появляется только тогда, когда на всех входах будет присутствовать логическая единица. То есть, и на первом, и на втором, и на третьем (если он есть), и на всех имеющихся входах. Если хотя бы на одном входе будет ноль, то и на выходе тоже будет ноль.
элемент «или», па выходе этого элемента появится логическая единица тогда, когда хотя бы на одном из входов появится единица. То есть, или на первом, или на втором, или на третьем — на любом из имеющихся входов. Логический ноль на выходе будет только тогда, когда на всех входах будет сигнал логического нуля.
элемент «нь». или инвертор, у этого элемента всегда один вход и один выход. И логика его работы очень проста. Когда на входе у инвертора сигнал логического нуля, на выходе — логическая единица. И наоборот, когда на входе логическая единица, на выходе логический ноль.
Составляя из этих трех основных кирпичиков различные схемы, мы можем получить все разнообразие цифровых и логических элементов, применяемых в микропроцессорной технике, которые в свою очередь имеют свои схемные обозначения и выглядят на схеме как самостоятельные элементы.
Для отображения логики работы того или иного элемента принято составлять так называемые таблицы истинности. Таблица истинности — это такая таблица, которая имеет столбцы для всех входов и выходов конкретного элемента. В строках таблицы отображаются все возможные состояния элемента. Каждая строка соответствует одному из возможных состояний. На рис. 5 приведены таблицы истинности для трех
основных логических элементов. Для наглядности в данном случае приведены трехвходовые варианты элемента «И» и элемента «ИЛИ».

Теперь попробуем сами составить более сложный элемент из нескольких простых. Для примера соединим элемент «И» с инвертором так, как это показано на рис. 6. В результате у нас получится новый элемент, также широко применяемый на практике. Этот элемент имеет свое название и схемное обозначение. Называется такой элемент «И-НЕ», а его схемное обозначение приведено на рис. 7. Подчеркиваю: на рис. 6 и на рис. 7 изображен по сути дела один и тот же логический элемент.
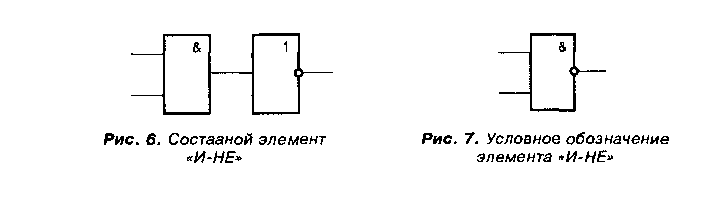
В реальной схеме могут применяться оба варианта: как готовая микросхема «И-НЕ», так и последовательное соединение элемента «И» и инвертора. Дело в том, что любая реальная микросхема обычно содержит несколько аналогичных логических элементов. Стандартный корпус микросхемы имеет 14 либо 16 выводов. Поэтому в одном корпусе
обычно размещают четыре двухвходовых элемента или три трехвходовых. Для рационального использования всех элементов (чтобы не оставалось неиспользованных) одну и ту же схему в разных случаях собирают по-разному.
Логика работы элемента «И-НЕ» очевидна. Сигнал на выходе будет равен нулю в том и только в том случае, когда на всех его входах присутствует логическая единица.
Попробуем теперь синтезировать более сложный логический элемент под названием «Исключающее ИЛИ». Его тоже часто можно встретить в различных электронных схемах.
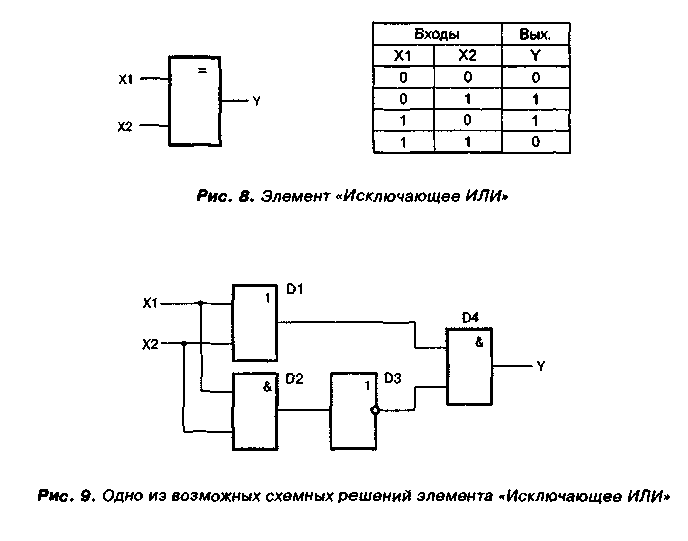
Схемное обозначение элемента «Исключающее ИЛИ» и его таблица истинности приведены на рис. 8. Как видно из таблицы, логика работы элемента соответствует его названию. Это тот же элемент «ИЛИ», за исключением того случая, когда на обоих входах присутствует логическая единица. В отличие от «ИЛИ», элемент «Исключающее ИЛИ» в этом случае формирует на выходе сигнал логического нуля.
Эквивалентная схема элемента «Исключающее ИЛИ» изображена на рис. 9. Советую самостоятельно разобрать работу этой схемы. Для этого мысленно нужно подставлять на входы XI и Х2 различные варианты логических сигналов и для каждого варианта проследить, какими будут сигналы на выходе каждого элемента и всей схемы.
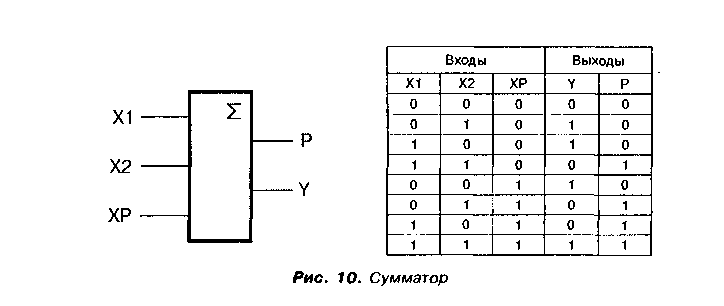
Если внимательно посмотреть на таблицу истинности элемента «Исключающее ИЛИ», то легко заметить, что логика работы элемента очень похожа на таблицу сложения двух одноразрядных двоичных чисел. И действительно: ноль плюс ноль равняется ноль. Один плюс ноль и ноль плюс один, равняется один. А сумма двух единиц дает ноль в этом разряде и единицу переноса в следующий разряд. Таким образом, не хватает только переноса. Элемент, который выполняет суммирование входных сигналов, называется сумматором. Его также можно составить из элементарных логических элементов. Схемное изображение и логика работы сумматора приводятся на рис. 10. Здесь XI и Х2 — это входы складываемых разрядов. У — выход суммы. Р — выход переноса в более старший разряд. ХР — вход переноса с младшего разряда. Для суммирования многоразрядных цифровых сигналов сумматоры соединяют каскадом. При этом сигнал с выхода Р сумматора одного разряда подается на вход ХР сумматора следующего разряда.
На практике отдельные микросхемы — сумматоры — почти никогда уже не применяются. Где-то внутри микропроцессора обязательно есть сумматор, который является его частью. Я привел его описание лишь, как пример сложного элемента цифровой техники.
При разработке микропроцессорных систем нам чаще придется иметь дело с другими элементами, такими, как триггеры, регистры, дешифраторы, мультиплексоры, и т.д. В следующих разделах мы рассмотрим подробнее все эти устройства.