Материал взят из книги

Скачать оригинал КНИГИ в хорошем качестве
Если вы всерьез собрались научиться разрабатывать микропроцессорные устройства, вам просто необходимо знать, как же компьютер хранит и обрабатывает числа. К сожалению (а может и к счастью) люди не придумали способа записывать при помощи электронных сигналов числа в том виде, как мы их привыкли видеть. Поэтому математикам сначала пришлось потрудиться и придумать другой, более подходящий способ их представления.
И они потрудились на славу! Придуман не один, а огромное множество способов представления чисел. Один из этих способов идеально подходит для реализации его при помощи электроники. Некоторые другие способы помогают удобнее представлять компьютерные данные
14 Я {эУМЯГ#» МПМ 14 Я к'ПХ.ШКЮТРПЯ
итак, что же это за спосооы.' люоои грамотный человек хорошо знает, по крайней мере, два способа представления чисел. Это, широко распространенные, арабские цифры и изредка применяемые римские. Одно и тоже число можно записать как 2 или как II, как 5 или как V, как 22 или как XXII. Очевидно, что перед нами два альтернативных способа написания чисел. Числа одинаковые, а способы написания разные.
му а если есть два спосооа, почему оы ни выдумать и третий, четвертый и т.д.? И математики давно нашли такие способы. И не три, четыре. Они нашли универсальный прием, позволяющий теоретически создавать бесконечное количество способов представления чисел. Эти способы назвали системами счисления.
За основу взяли арабские числа. Очевидно, что этот способ представления гораздо более красивый, чем римский, так как подчиняется строгому закону. Судите сами. В привычной для нас системе счисления мы имеем 10 цифр: I, 2, 3, 4, 5, 6, 7, 8, 9 и 0. При помощи этих цифр мы легко можем представить любое число. Для представления чисел меньших десяти мы используем одну из этих десяти цифр. Для представления чисел от десяти и выше мы вводим новый разряд, который для начала приравниваем к единице. Подставляя в младший разряд по порядку те же десять базовых цифр, мы получаем следующий десяток. Как только все цифры в младшем разряде перебраны, мы увеличиваем наш старший разряд на единицу.
И так, пока не переберем все цифры вплоть до 99. Когда во втором разряде будут перебраны все цифры, мы вводим третий разряд. И так далее. Внимательно изучив, как мы строим числа, мы можем сформулировать набор четких правил, как при помощи десяти знаков, означающих десять цифр, представить любое мыслимое число! Такая система счисления называется десятичной. Так как количество цифр, используемое для представления чисел, равно десяти.
Вот тут-то и кроется простое, но гениальное решение. А почему именно десять цифр? Видимо потому, что первобытные люди, которые изобретали эту систему, пользовались для счета пальцами рук. А их всего десять. А если бы природа распорядилась так, что у человека было бы, не по пять, а по четыре пальца на каждой руке? Тогда, наверно, мы бы имели восьмеричную систему счисления! И как же такая система будет выглядеть? Ну, во-первых, она будет иметь только восемь цифр. Например: 0, 1,2, 3, 4, 5, 6 и 7. Ну а правила построения чисел, мы оставим те же. Числа от нуля до восьми мы запишем так же, как и в десятичной системе.
Цифры 8 в восьмеричной системе нет. Поэтому мы поступим в строгом соответствии с правилами. Мы добавим новый разряд и запишем туда единицу. А в младшем у нас будет ноль. При этом число 8 в восьмеричной системе счисления будет выглядеть как 10. В математике придуман способ записи чисел в различных системах счисления, так, что бы было ясно в какой системе число записано. Десятичную систему еще называют системой счисления по основанию десять. А восмеричная система — это, в свою очередь, система счисления по основанию восемь. Так вот, число восемь в десятичной системе записывается так: 810. А то же число в восьмеричной системе записывается следующим образом: 108. Маленькая цифра в конце числа соответствует основанию системы счисления, в которой данное число записано.
Продолжим записывать числа в восьмеричной системе счисления, сравнивая их с теми же числами, записанными в десятичном виде:
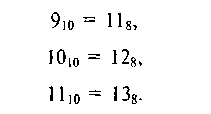
И так далее, пока не кончится наш набор цифр.
Число 1510 записывается, как 178.
А вот число 16,о запишется уже как 208.
То есть снова и снова выполняется одно из стандартных правил построения чисел: как только значение любого из разрядов доходит до своего максимума, значение старшего по отношению к нему разряда увеличивается на единицу, а значение текущего разряда устанавливается равным нулю.
Используя вышеописанные правила, теоретически можно построиті систему счисления по любому основанию. Лишь бы хватило значков обозначающих цифры. Реально же на практике нашли применения кроме десятичной, восьмеричная, шестнадцатеричная и двоичная системы счисления. Причем, именно двоичная система счисления и является той самой системой представления чисел, которую инженеры бе: труда смогли смоделировать при помощи электронных схем. Восьмеричная и шестнадцатеричная системы счисления очень удобны для записи компьютерных данных на бумаге и на экране компьютера. Раньше, на заре развития компьютерной техники, широко использовал? восьмеричную систему. Сейчас она почти забыта. Теперь вместо нее более употребима шестнадцатеричная система счисления.
Разберем по подробнее две еще не описанные нами системы. В шестнадцатеричной системе счисления, как вы догадались, используете? шестнадцать цифр. Обычно в качестве десяти первых цифр применяю! обычные цифры из десятичной системы. А недостающие шесть циф( заменяют буквами латинского алфавита. Вот полный набор цифр шест-
Посмотрите несколько примеров записи чисел в восьмеричной системе счисления:

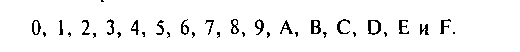
При помощи одного разряда в шестнадцатеричной системе счисления можно записать числа от нуля до пятнадцати. Число шестнадцать (1610) записывается, как 10)6- Вот еще несколько примеров шестнадцатеричных чисел:
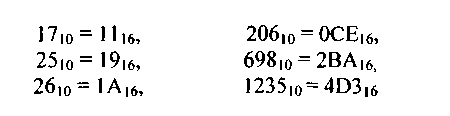
Для того, чтобы было легче отличать число, записанное в шестнадцатеричной системе от слова, перед шестнадцатеричным числом, начинающимся с буквы, принято ставить ноль. Такое правило актуально в основном в случае написания текстов для программ, для облегчения машинного распознавания. Но к этому мы еще вернемся. А сейчас продолжим изучение нашей темы.
Среди всех систем счисления особое место занимает двоичная'система. Она использует для записи любого числа всего две цифры. Это цифры 0 и 1. Естественно, что при помощи одного разряда, в двоичной системе можно записать только два числа: 0 и 1. Число два в двоичной системе будет выглядеть как 102. Используя уже знакомые правила, запишем другие числа:
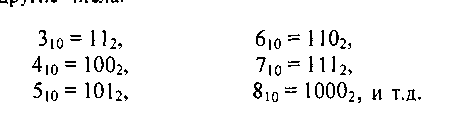
Если у вас есть компьютер, на котором установлен Windows, вы сами легко можете поэкспериментировать с переводом чисел из одной системы счисления в другую. Для этого запустите стандартный калькулятор, входящий в Windows. Обычно он запускается через меню Пуск -» Стандартные -> Калькулятор. Войдите в меню «Вид» калькулятора и выберите «Инженерный^. После этого вид калькулятора изменится. Вы увидите дополнительные буквенные клавиши для набора латинских букв. А в левой верхней части калькулятора появится переключатель систем счисления. Он имеет четыре положения: Hex (шестнадцатеричная), Dec (десятичная), Oct (восьмеричная) и Bin (двоичная).
Вы можете выбрать любую из систем счисления, набрать на калькуляторе число, а затем переключить калькулятор на любую другую систему. Калькулятор тут же, автоматически, переведет набранное вами число в новую систему счисления. Советую поэкспериментировать, таким образом, стараясь лучше понять, почему так, а не иначе представляется то или иное число в разных системах счисления.
о различных языках программирования применяется другие спосооы записи чисел в различных системах счисления. Самый распространенный способ — добавление в конце числа латинской буквы, обозначающей систему счисления. Так, для обозначения шестнадцатеричных чисел используется буква Н, для восьмеричных — буква О, для двоичной системы — буква В. Десятичные числа при этом можно записывать либо вообще без буквы, либо с буквой О. Приведем примеры записи чисел в этой Фопме:
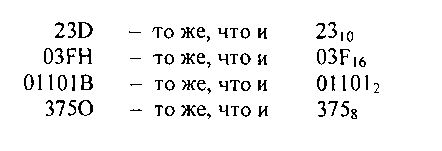
Альтернативный способ написания чисел хорош тем, что не использует специальных эффектов типа нижнего индекса, и поэтому может быть использован при наборе текста в любом простейшем редакторе.
Во всех вышеперечисленных системах счисления возможны все арифметические операции, к которым мы привыкли в десятичной системе. То есть сложение, вычитание, умножение, деление. Правда на практике, никто не занимается восьмеричной и шестнадцатеричной арифметикой. Это не имеет никакого смысла. А вот арифметика в двоичной системе была подробно проработана. Надо же было обучить этому электронные устройства.
Возьмем, например, сложение. В двоичной системе счисления оно делается точно так же, как и в десятичной. Только нужно помнить, что в этой системе каждый разряд может принимать лишь два значения: либо О, либо 1. Возьмем два двоичных числа и найдем их сумму. Например, 10011001110 +11000101110. Точно так же, как и в десятичной системе, складываем числа поразрядно, начиная с младшего разряда. Ноль плюс ноль получится, естественно, ноль. Один плюс ноль и ноль плюс один дадут в результате единицу. При сложении двух единиц мы получим ноль в этом разряде и единицу переноса в следующий разряд. Вот результат
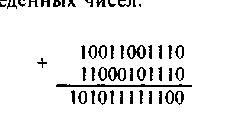
Умножение тоже делается аналогично умножению в десятичной системе — столбиком. При этом очевидно, что любое число, умноженное на ноль, дает в результате ноль. А число, умноженное на единицу, дает в результате то же самое число. Вот пример умножения столбиком двух двоичных чисел: полученных сдвигом чисел. Точно также легко убедиться, что деление в двоичной системе сводится к сдвигу и вычитанию. Это важно при построении вычислительных устройств. Именно поэтому многие простые микропроцессоры не имеют в составе своих команд, команд умножения и деления. Но обязательно, каждый процессор имеет команды сдвига, сложения и вычитания. Если программисту по ходу программы понадобится умножить либо поделить два числа, он всегда может составить небольшую подпрограмму, используя команды сдвига сложения и вычитания.
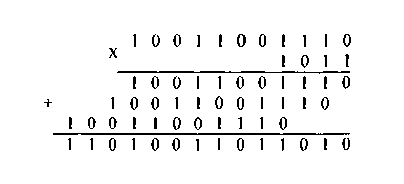
Как легко убедиться из примера, умножение в двоичной системе счисления сводится к сдвигу первого числа (множимого) влево и сложению,